Trigonometry : Concept of Measurement of Angle

Exercise 20

1. Let us express the following into degrees, minutes, and seconds.

(i) 832’     (ii) 6312”    (iii) 375”
(iv) 27 (1/12)^o    (v) 72.04^o

2. Let us determine the circular values of the followings.

(I) 60^o  (ii) 135^o 
(iii) -150^o   (iv) 72^o 
(v) 22^o 30’  (vi) -62^o 30’ 
(vii) 52^o 52’30” 
(viii) 40^o 16’24”

3. In ΔABC, AC = BC and BC is extended upto the point D. If ∠ACD = 144 , then let us determine the circular value of each of the angles od ∠ABC.

4. If the difference of two acute angle of a right-angled triangle is 2π/5, then let us write the sexagesimal values of two angles.

5. The measure of one angle of a triangle is 65^o and other angle is π/12, then let us write the sexagesimal value and circular value of third angle.

6. If the sum of two angles is 135^o and their difference π/12, then let us determine the sexagesimal value and circular value of two angles.

7. If the ratio of three angles of a triangle is 2:3:4, then let us determine the circular value of the greatest angle.

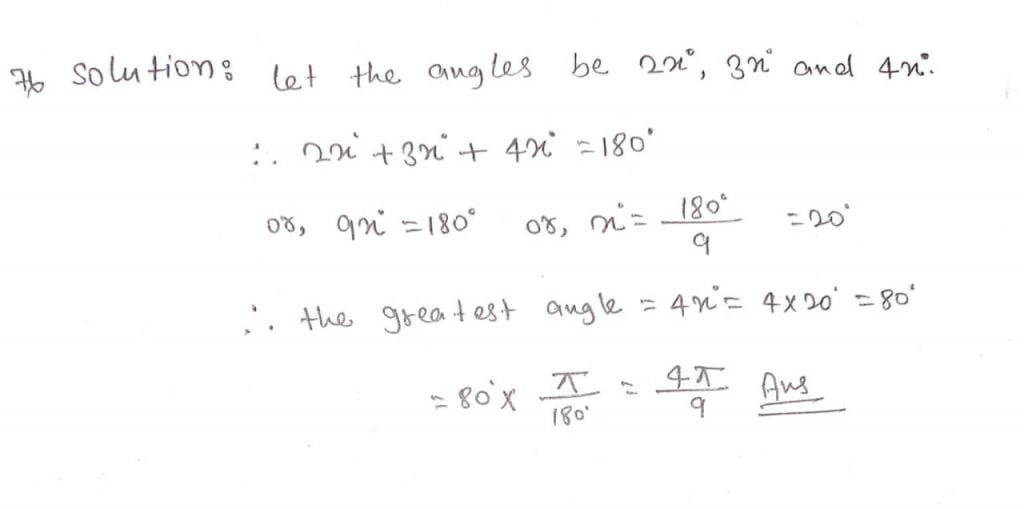
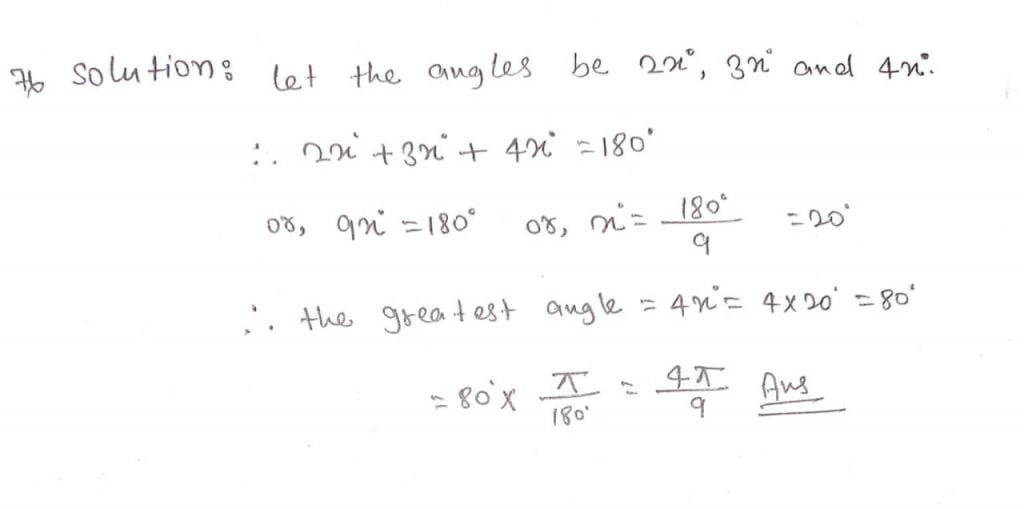
8. The length of a value radius of a circle is 28cm. Let us determine the circular value of angle subtended by an arc of 5.5 cm length at the center of this circle.

9. The ratio of two angles subtended by arc of unequal length at the centre is 5:2 and if the sexagesimal value of the second angle is 30^o , then let us determine the sexagesimal value and the circular value of the first angle.

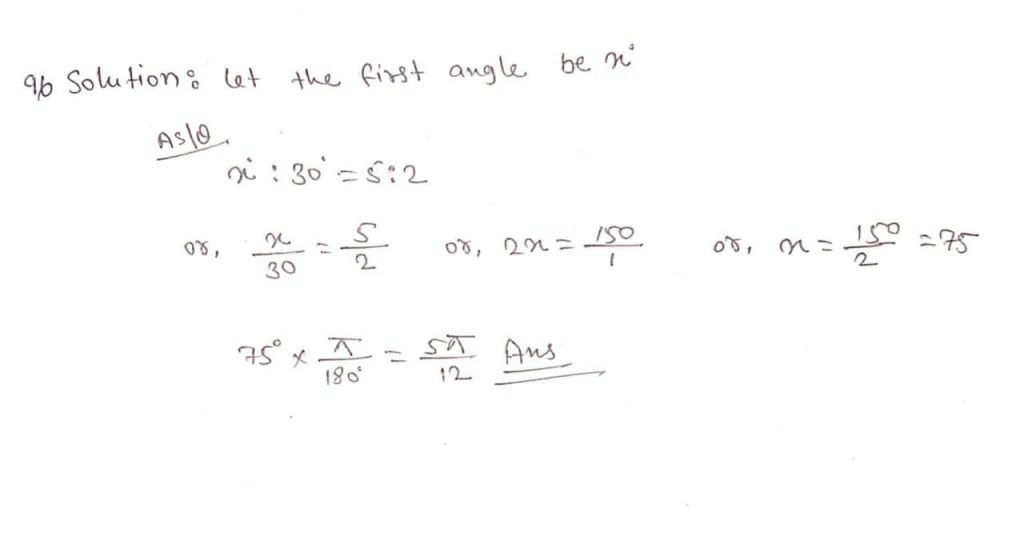
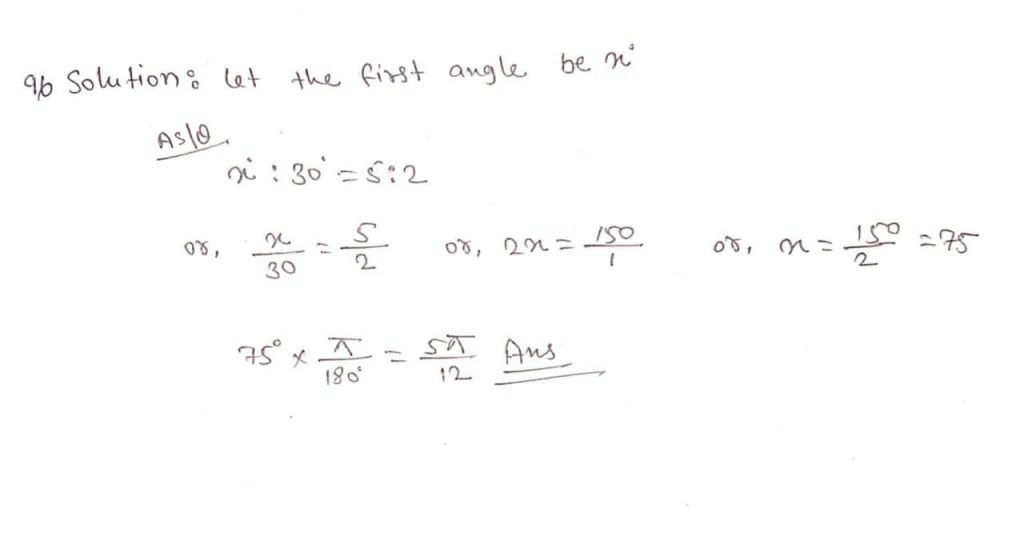
10. A rotating ray makes an angle -5 1/12π. Let us write by calculating, in which direction the ray has completely rotated and there after what more angle it has produced.

11. I have drawn
an isosceles triangle ABC whose included angle of two equal sides is ∠ABC = 45^o ; the bisector of ∠ABC intersects the side AC at the point D. Let us
determine circular values of ∠ABD  ∠BAD, ∠CBD, and ∠BCD.

12. The base BC of the equilateral triangle ABC is extended upto the point E so that CE = BC by joining A, E, let us determine the circular values of the angles of triangle ΔABC.

13. If the measure of three angles of quadrilateral are π/3, 5π/6 and 90^o respectively, then let us determine and write the sexagesimal and circular values of fourth angle.