Q1. If the length of the radius of a sphere is 10.5 cm, let us write by calculating the whole surface area of the sphere.


Q2. If the cost of making a leather ball is ₹ 431.20 at 17.50 per square cm, let us write by calculating the length of diameter of the ball.


Q3. If the length of diameter of the ball used for playing shotput in our school is 7 cm, let us write by calculating how many cubic cm of iron is there in the ball.


Q4. If the length of diameter of a solid sphere is 28 cm, and it is completely immersed into the water, let us calculate the volume of water displaced by the sphere.
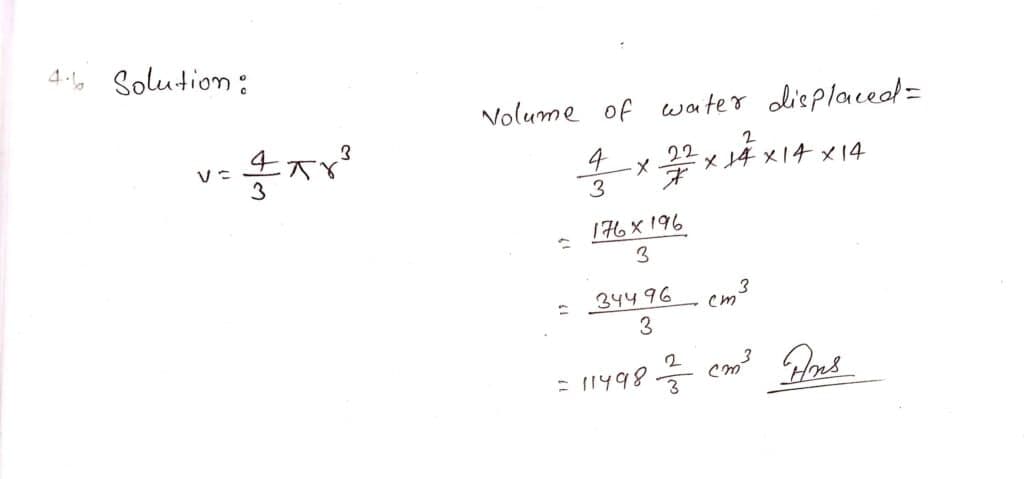
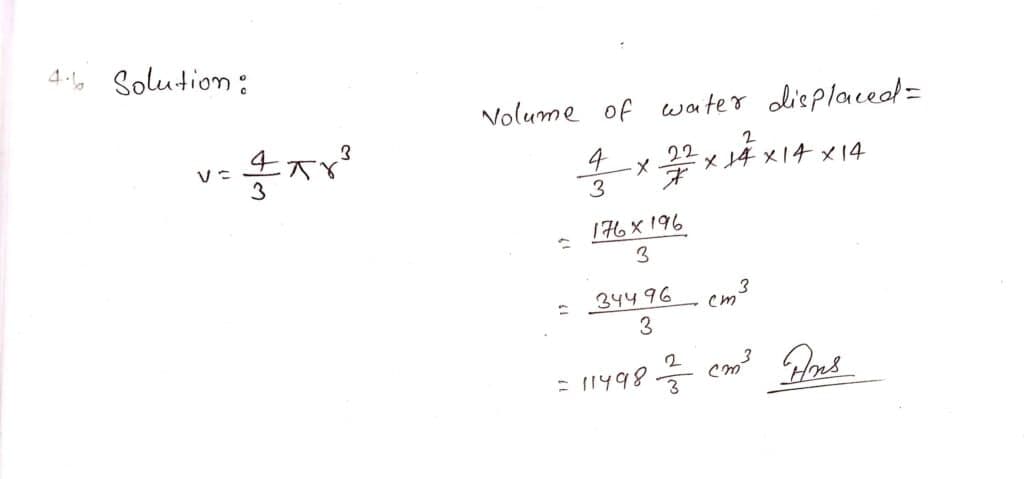
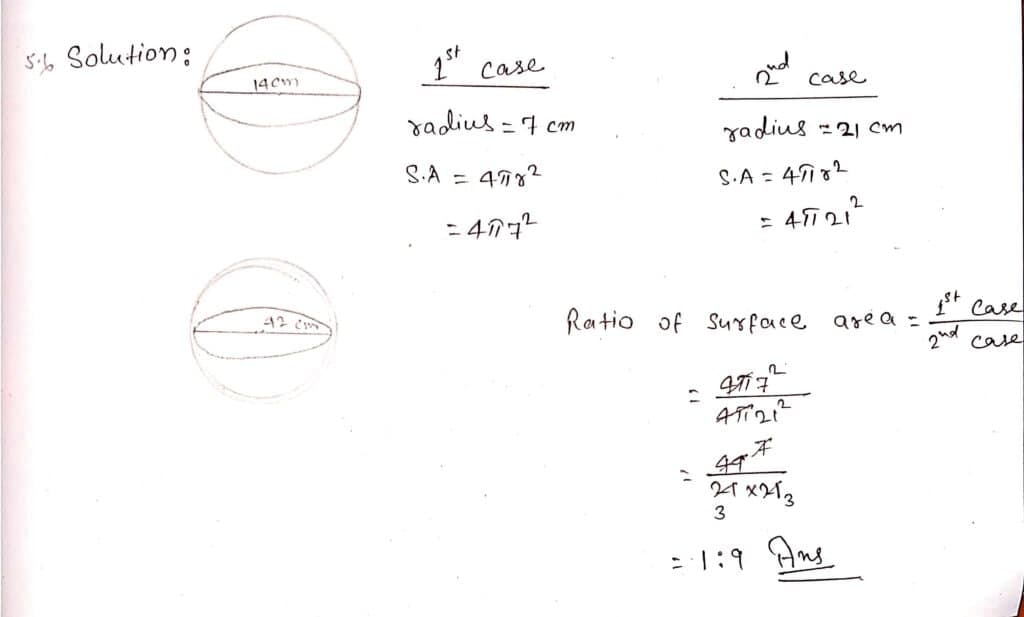
Q5. The length of radius of spherical gas balloon increases from 7 cm to 21 cm as air is being pumped into it let us find the ratio of surface area of the balloon in two cases.

Q6. 127 2/7 sq cm of sheet is required to make a hemispherical bowl. Let us write by calculating the length of diameter of the forepart of the bowl.


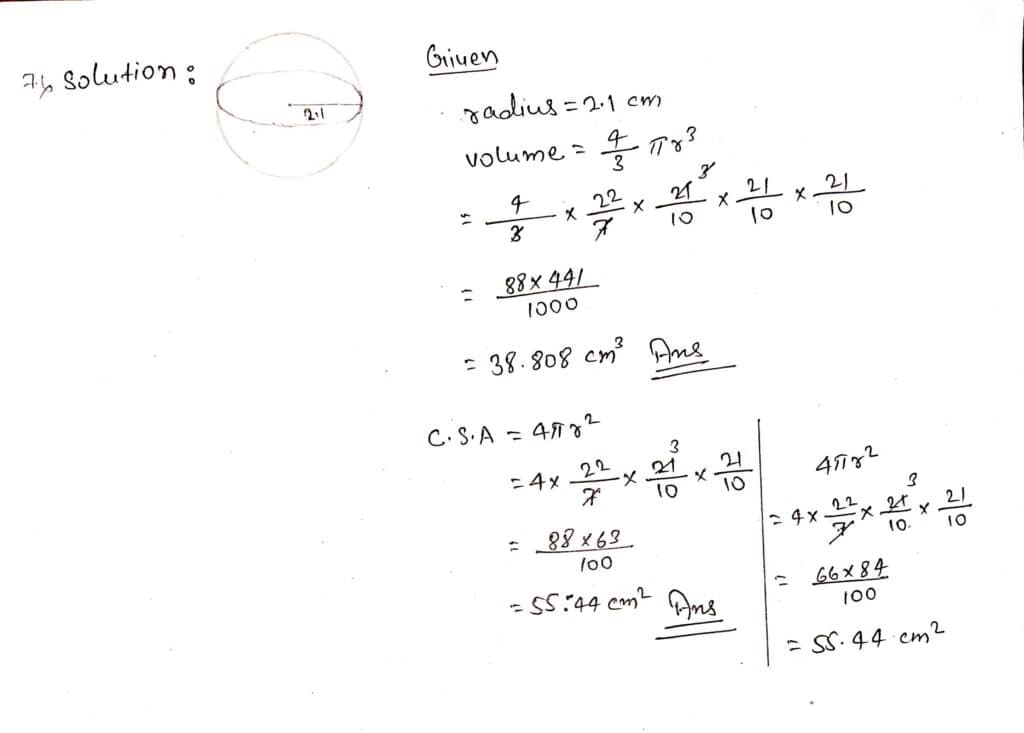
Q7. The length of radius of solid spherical ball is 2.1 cm; let us write by calculating how much cubic cm iron is there and let us find the curved surface area of the iron ball.

Q8. The length of diameter of solid sphere of lead is 14 cm. if the sphere is melted, let us write by calculating how many spheres with length of 3.5 cm radius can be made.


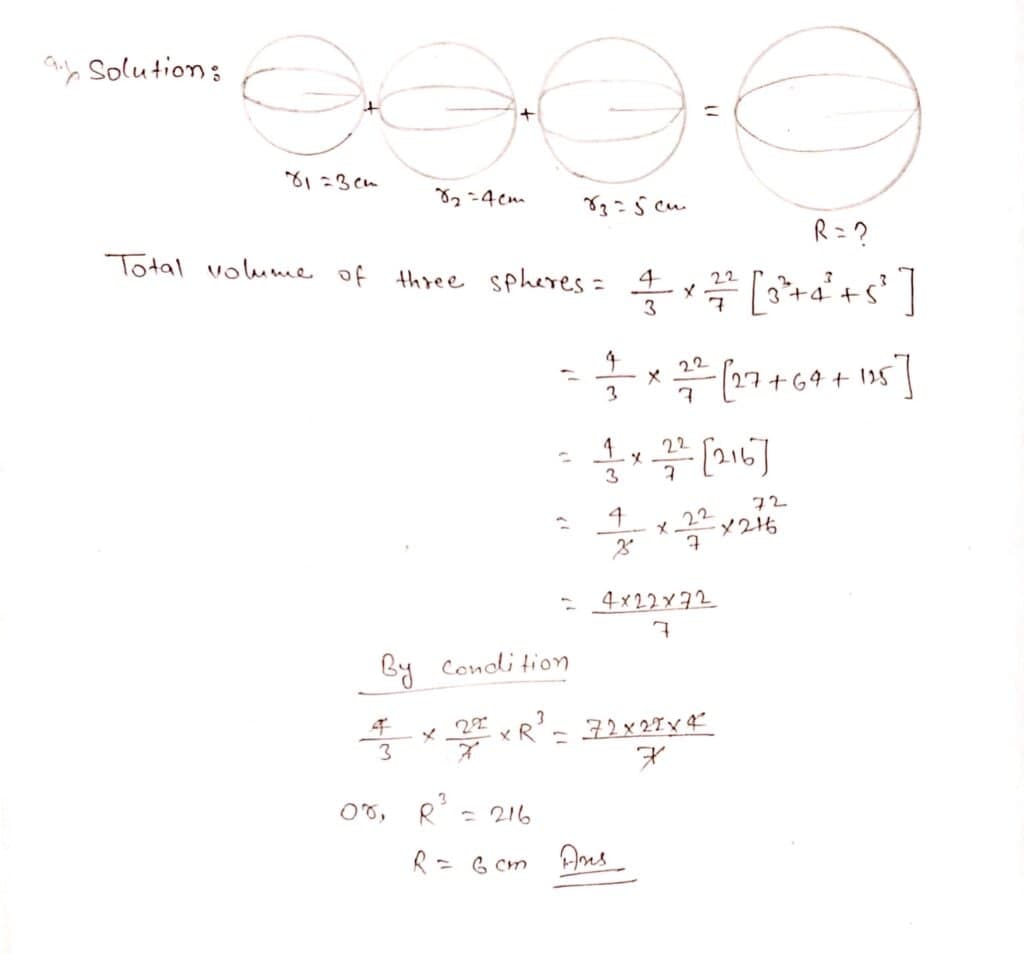
Q9. Three spheres made of copper having the length of 3 cm, 4 cm, and 5 cm radii are milted and a large sphere is made. Let us write by calculating the length of radius of the large sphere.

Q10. The length of diameter of base of a hemispherical tomb is 42 dm. let us write by calculating the cost of coloring the upper surface of the tomb at the rate of 35 per square meter.


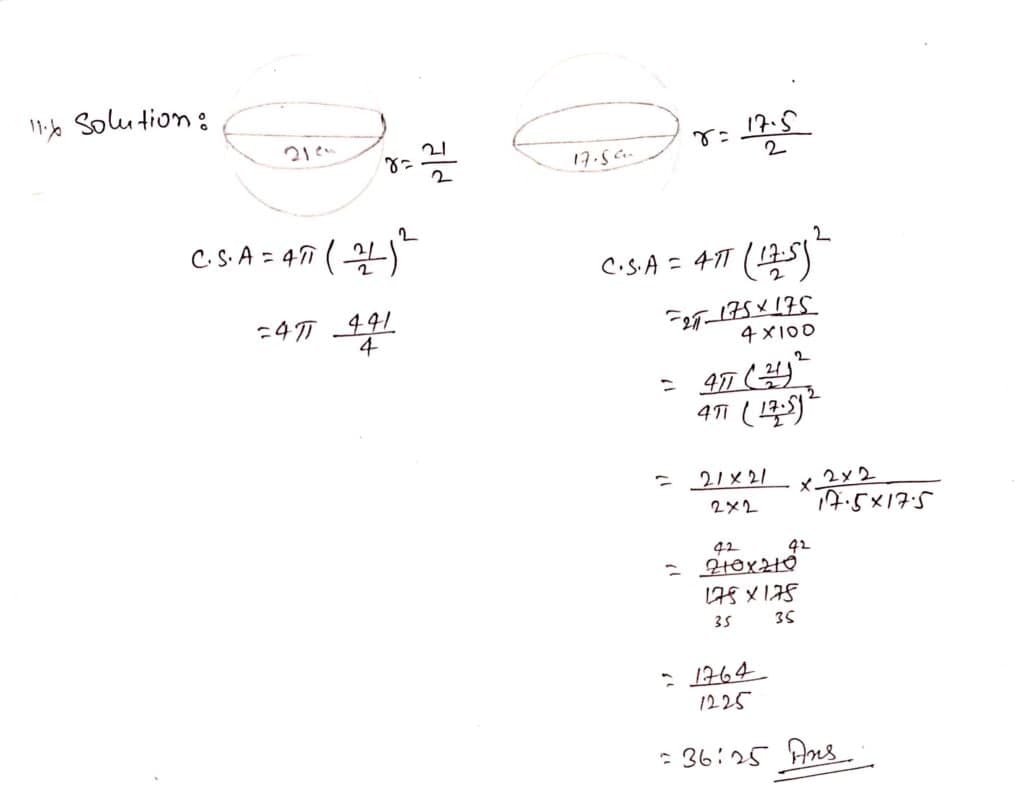
Q11. Two hollow sphere with the length of diameter 21 cm and 17.5 cm respectively are made from the sheets of the same metal. Let us calculate the ratio of the volumes of the potion cut off and the remaining portion of the sphere.

Q12. The curved surface of a solid metallic sphere is out in such a way that the curved surface area of the new sphere is half of that previous one. Let us calculate the ratio of the volumes of the portion of the sphere.


Q13. On the curved surface of the axis of a globe with the length of 14 cm radius, two circular holes ate made each of which has the length of radius 0.7 cm. Let us calculate the area of metal sheet surrounding its curved surface.


Q14. Let us write by calculating how many marbles with lengths of 1 cm radius may be formed by melting a solid sphere of iron having 8 cm length of radius.



