1. Choose the correct answer:
(i) If the ratio of principal and yearly amount be in the ratio 25 : 28, then the yearly rate of interest is
(a) 3%
(b) 12% (Ans)
(c) 105/7%
(d) 8%


(ii) Under what condition one root of the quadratic equation ax²+bx+c=0 is zero?
(b) a = 0
(b) b = 0
(c) c = 0 (Ans)
(d) None of these
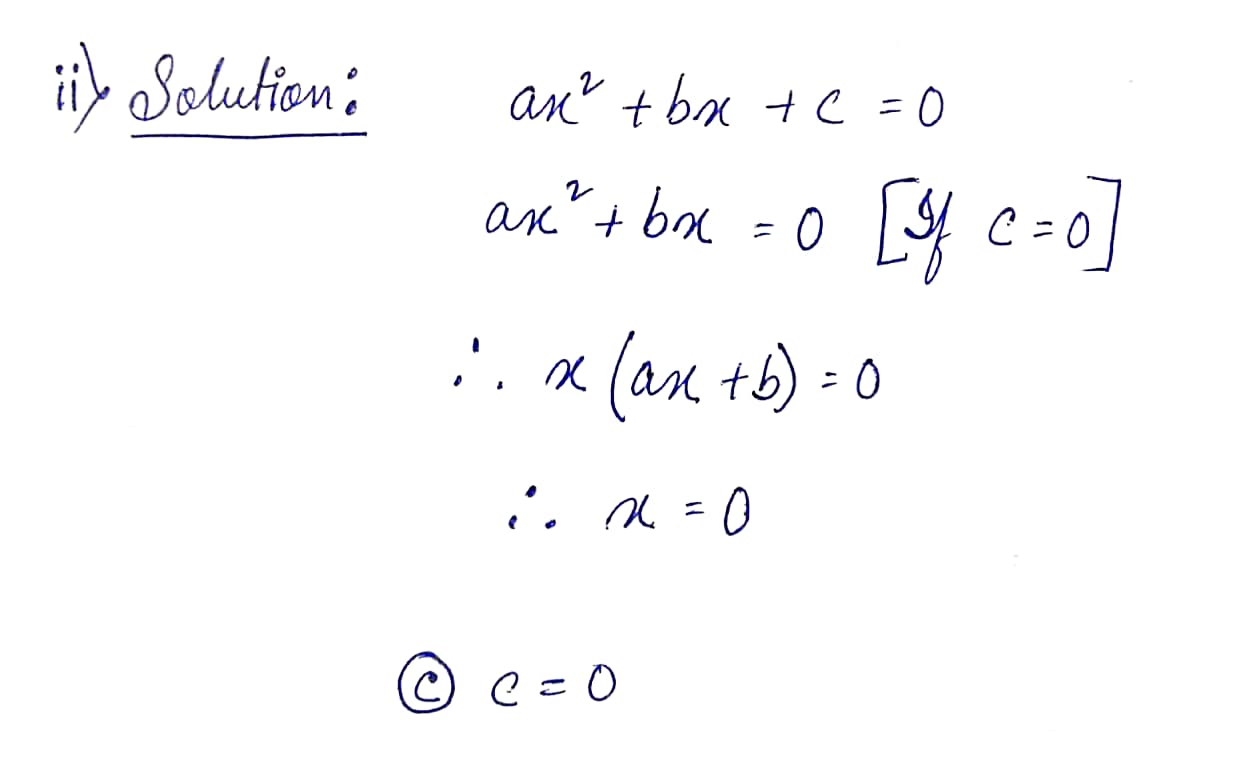
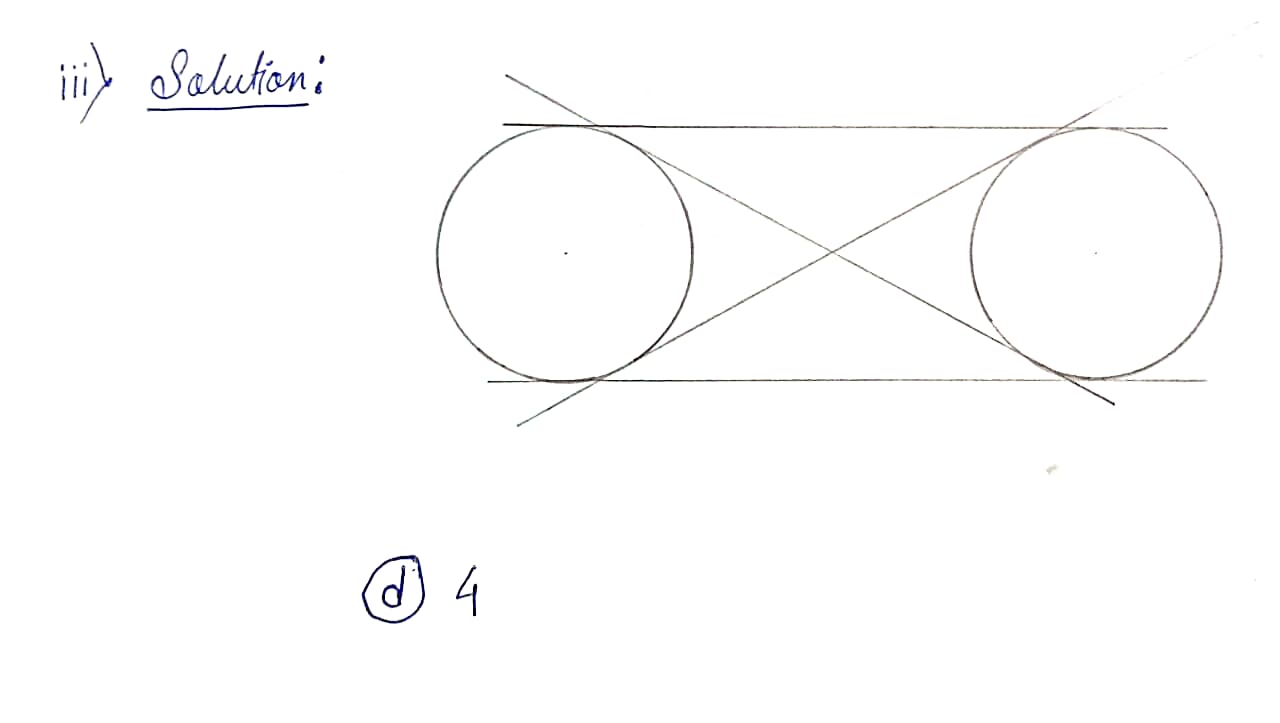
(iii) The number of common tangents of two circles when they do not touch or intersect each other is
(a) 2
(b) 1
(c) 3
(d) 4 (Ans)

(iv) If sin θ = cos θ, then the value of 2θ will be
(a) 30°
(b) 60°
(c) 45°
(d) 90° (Ans)


(v) If each of radius of the base and height of a cone be doubled, then the volume of it will be
(a) 3 times
(b) 4 times
(c) 6 times
(d) 8 times of the previous one (Ans)


(vi) The median of the numbers 2, 8, 2, 3, 8, 5, 9, 5, 6 is
(a) 8
(b) 6.5
(c) 5.5
(d) 5 (Ans)


2. Fill in the blanks (any five):
(i) At same rate per cent per annum, the simple interest and compound interest of same principal are same in one year.
(ii) If in a quadratic equation ax² + bx + c = 0 (a ≠ 0) b² = 4ac, then the roots of the equation will be real and equal.
(iii) It the length of the sides of two triangles are in proportion, then two triangles are similar.
(iv) If cos²θ – sin²θ = 1/x (x > 1), the cos⁴θ – sin⁴θ = 1/x.
(v) The numbers of plane surface of a solid hemisphere are 1.
(vi) If the mean of x1, x2, x3, x4 …… xn be x , then the mean of Kx1, Kx2, Kx3…….. Kxn is Kx. (K ≠ 0).
3. Write True or False (any five):
(i) A starts a business with Rs. 10,000 and B gives Rs. 20,000 after 6 months. At the end of the year their profit will be equal.
Ans: True


(ii) If x=2+√3, the value of x+1/x is 2√3.
Ans: False


(iii) If two circles of radii 7 cm and 3 cm touch each other. externally, then the distance between their centres will be 4 cm.
Ans: False


(iv) If 0° < θ < 90°, then sin sin θ > sin2 θ.
Ans: True


(v) If the total surface area of a hemisphere be 36π sq. cm., then its radius will be 3 cm.
Ans: False


(vi) If the perpendicular drawn on x-axis from the point of intersection of both ogive, the abscissa of the point of intersection of this perpendicular with the x-axis will be the median.
Ans: True
4. Answer the following questions (any ten):
(i) A sum of money is doubled in 8 years at r% rate of compound interest per annum. At the same rate in how many years it will be four times of the sum?
Ans:


(ii) A invests 1½ times more than B invests in a business. At the end of the year B receives Rs. 1,500 as profit. How much profit A will get at the end of that year?
Ans:
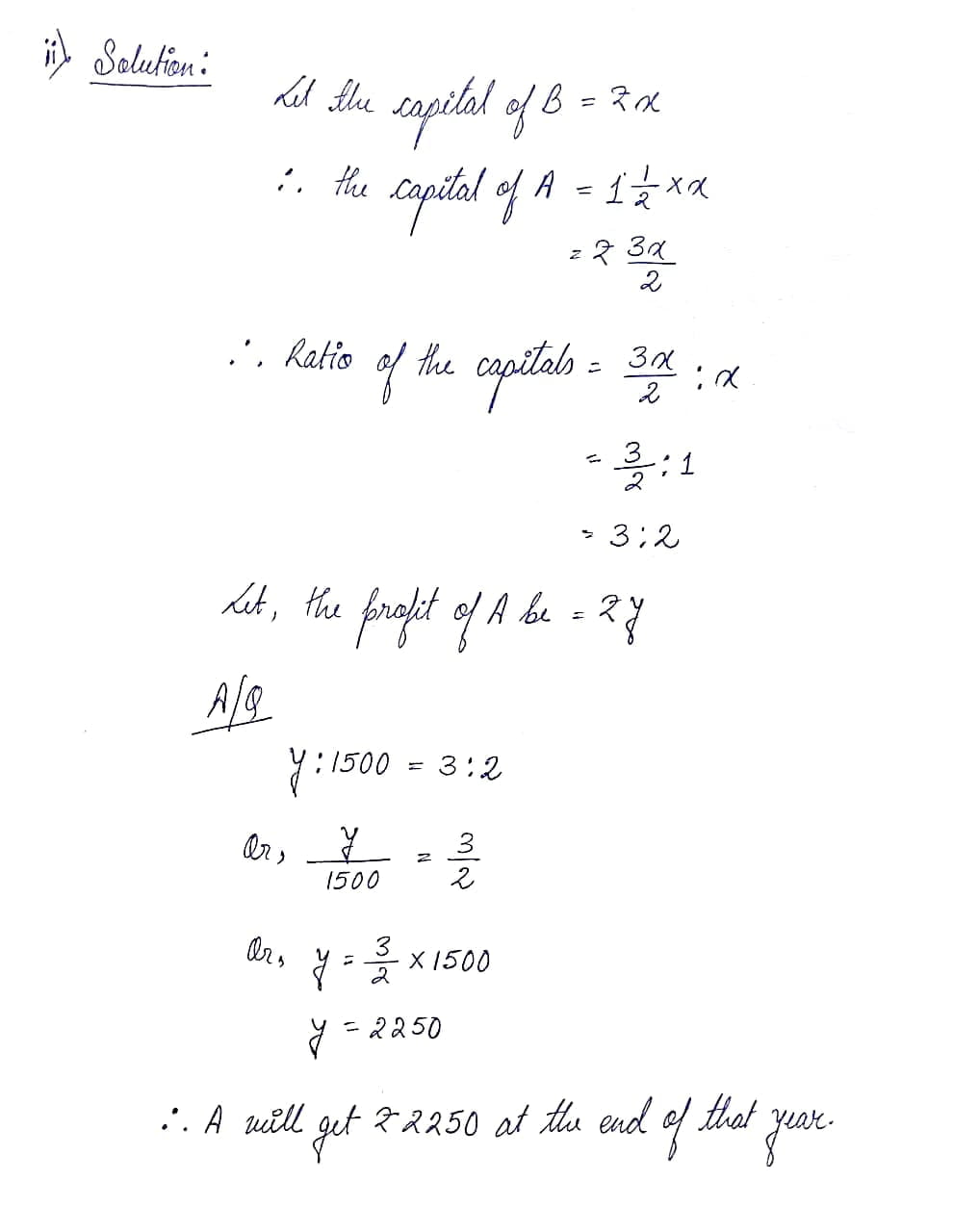
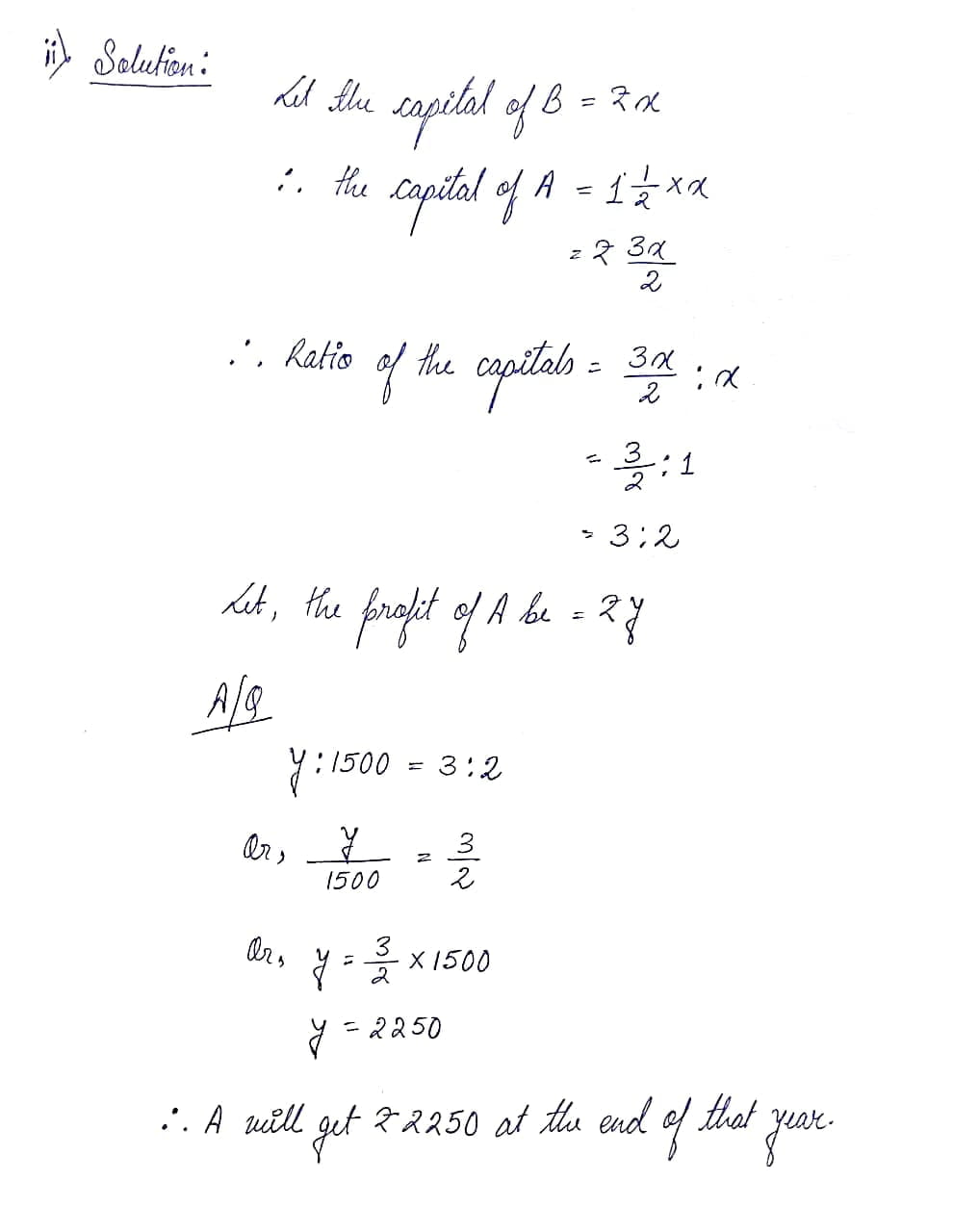
(iii) Without solving, find the values of ‘p’ for which the equation x²+(p-3)x+p=0 has real and equal roots.
Ans:
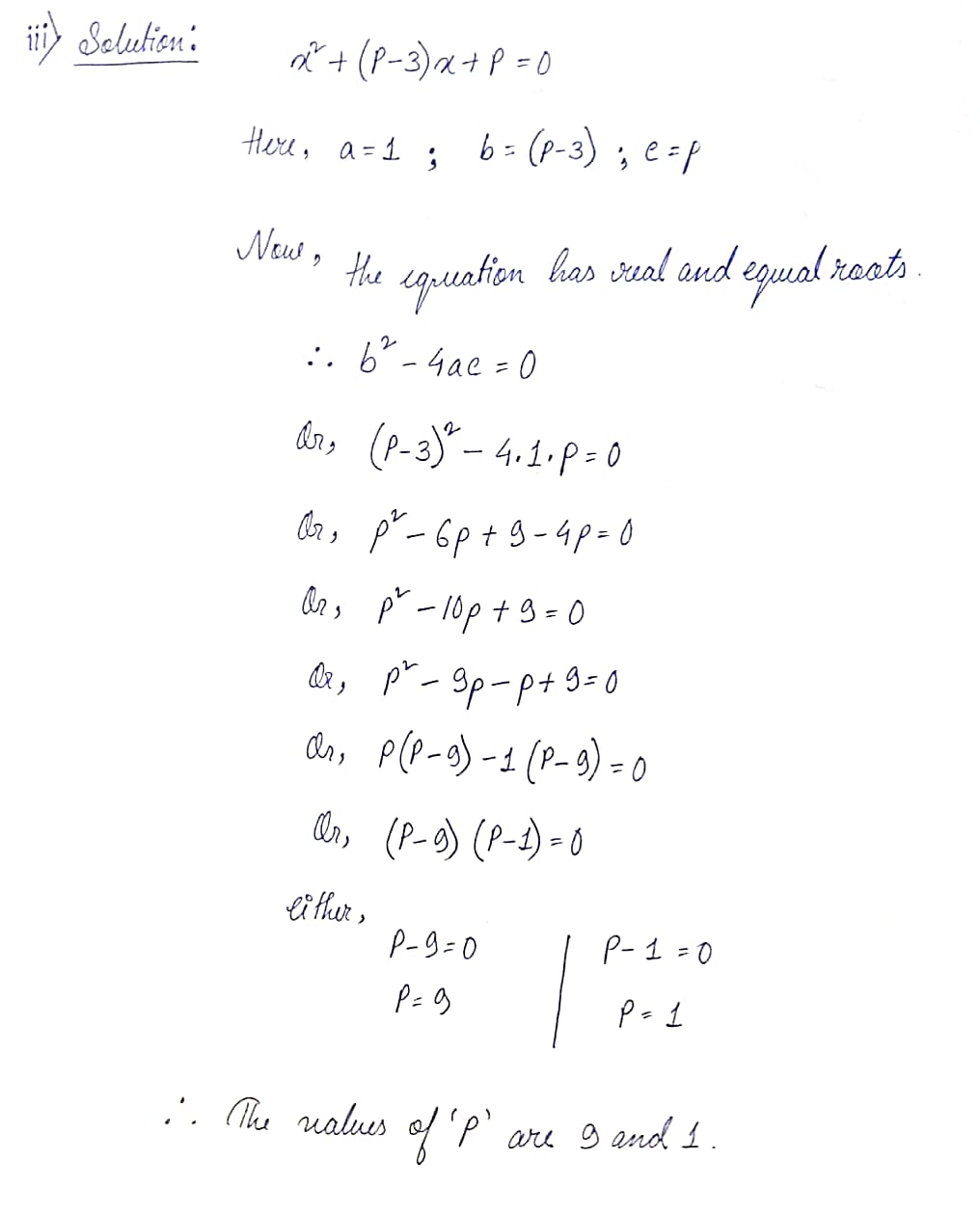
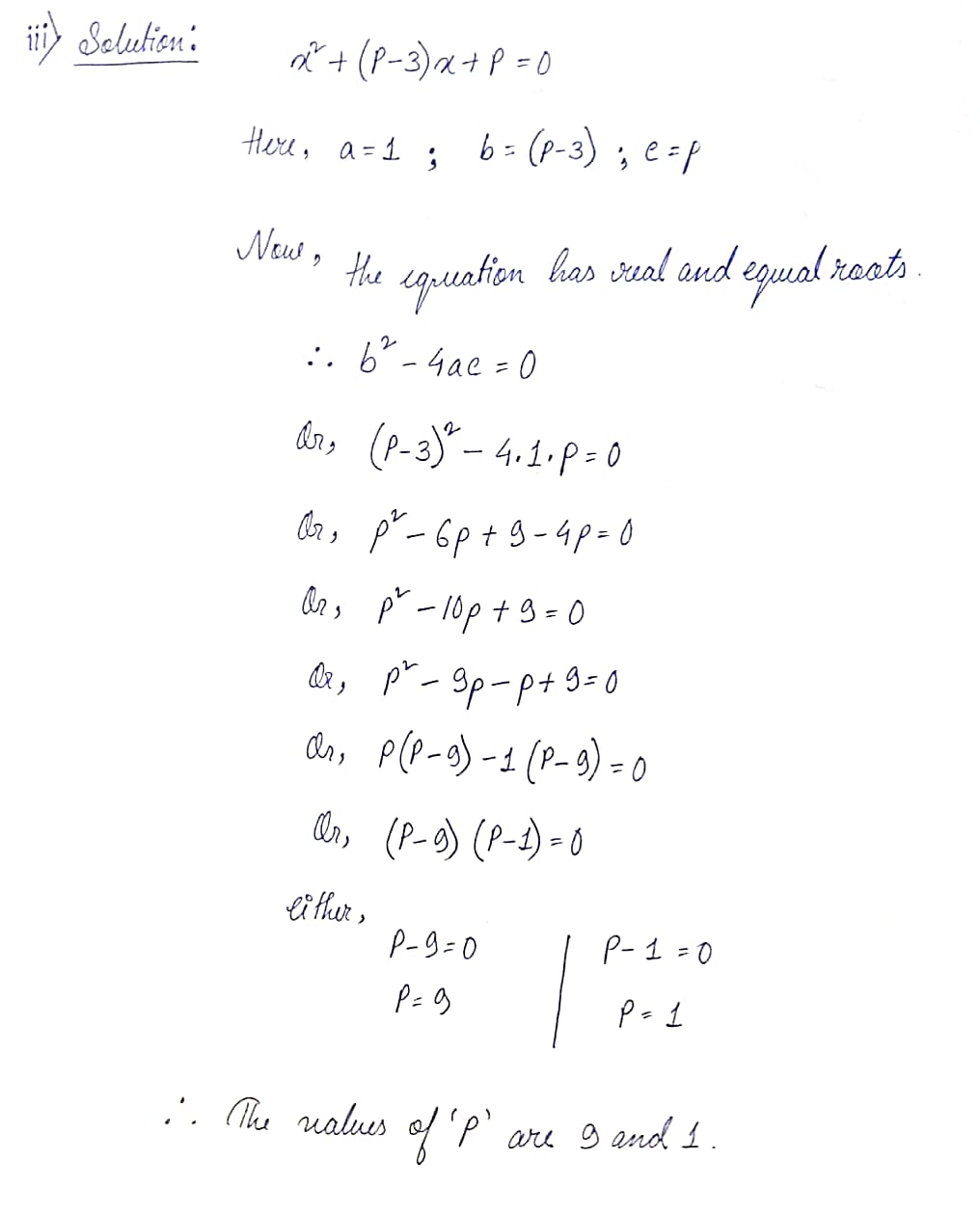
(iv) If x ∝ yz and y ∝ x show that z is a non-zero constant.
Ans:


(v) The perimeter of two similar triangles are 20 cm and 16 cm respectively. If the length of one side of the first triangle is 9 cm, then find the length of corresponding side of second triangle.
Ans:
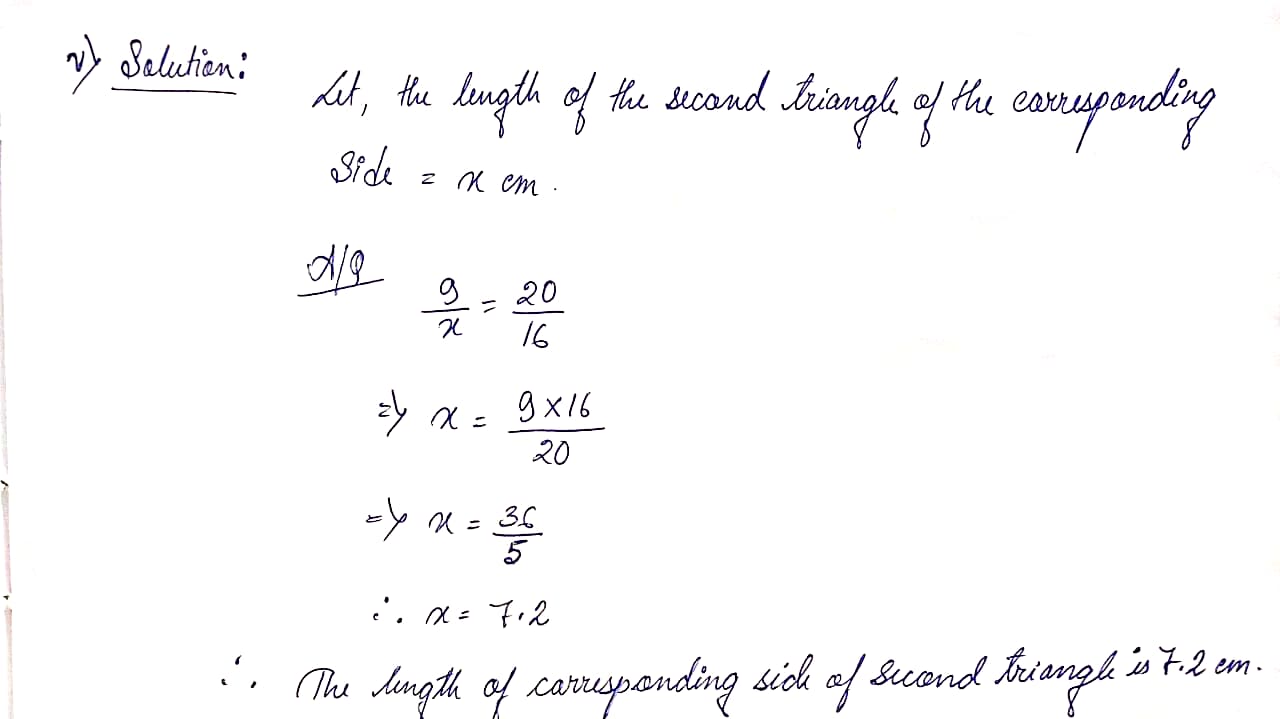
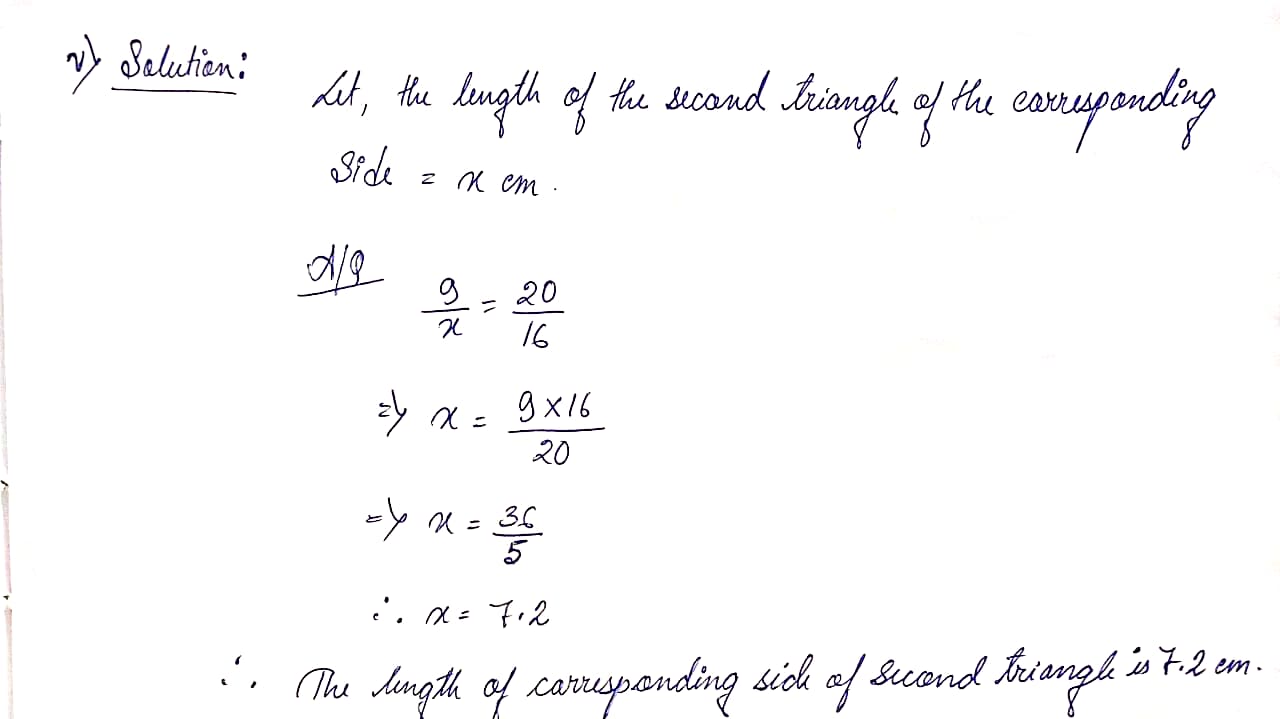
(vi) In Δ ABC, Δ ABC 90°, AB = 5 cm, BC = 12 cm. Find the length of the circumradius of Δ ABC.
Ans:


(vii) In Δ ABC, If AB = (2a – 1) cm, AC = 2√2a cm and BC = (2a + 1) cm, then write down the value of ∠ABC.


(viii) If x = a sec θ and y = b tan θ, then find the relation between x and y free from θ.
Ans:


(ix) If tan (θ + 15°) = √3 , find the value of sin θ + cos θ.
Ans:


(x) The diameter of one sphere is double the diameter of another sphere. If the numerical value of total surface area of larger sphere is equal to the volume of smaller sphere, then find the radius of the smaller sphere.
Ans:


(xi) If the number of surfaces of a cuboid is x, the number of edges is y, the number of vertices is z and the number of diagonals is P, then find the value of x – y + z + P.
Ans:


(xii) If 11, 12, 14, x – 2, x + 4, x + 9, 32, 38, 47 are arranged in ascending order and their median is 24, find x.


5. Answer any one question :
(i) The difference between simple interest and compound interest for 2 years of a sum of money becomes Rs. 80 at 4% interest per annum. Calculate the sum of money.
Ans:
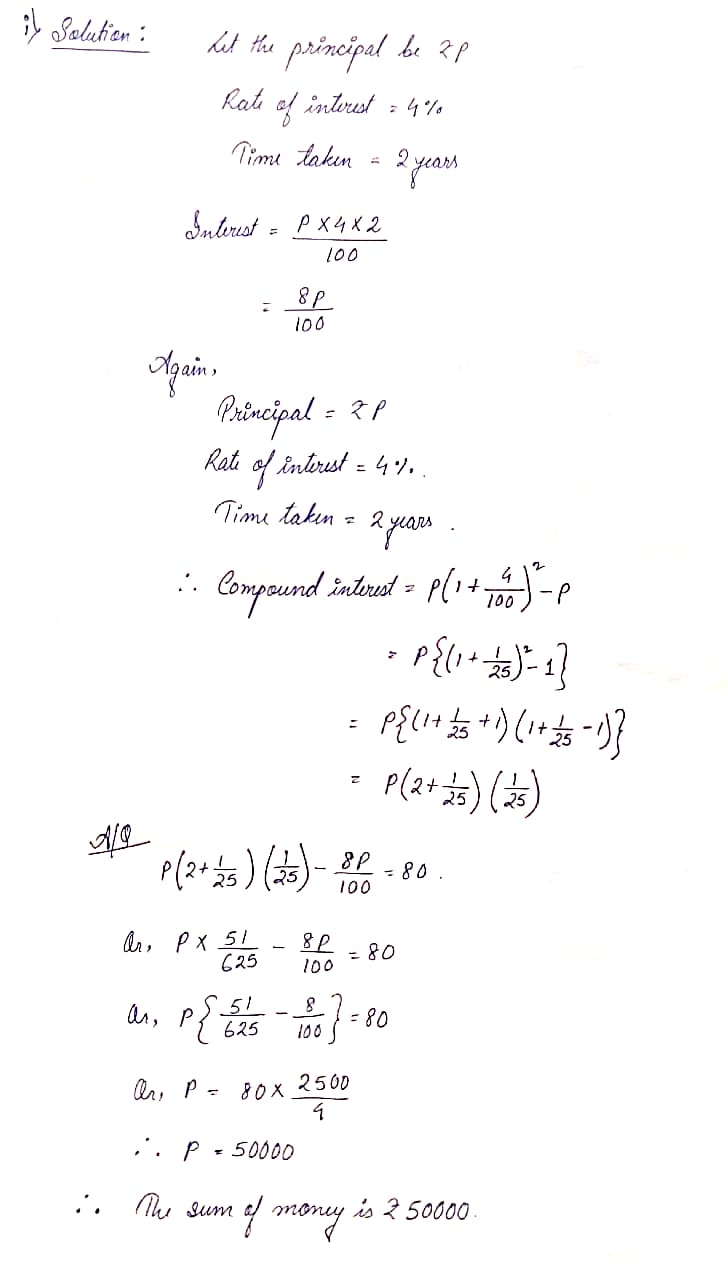
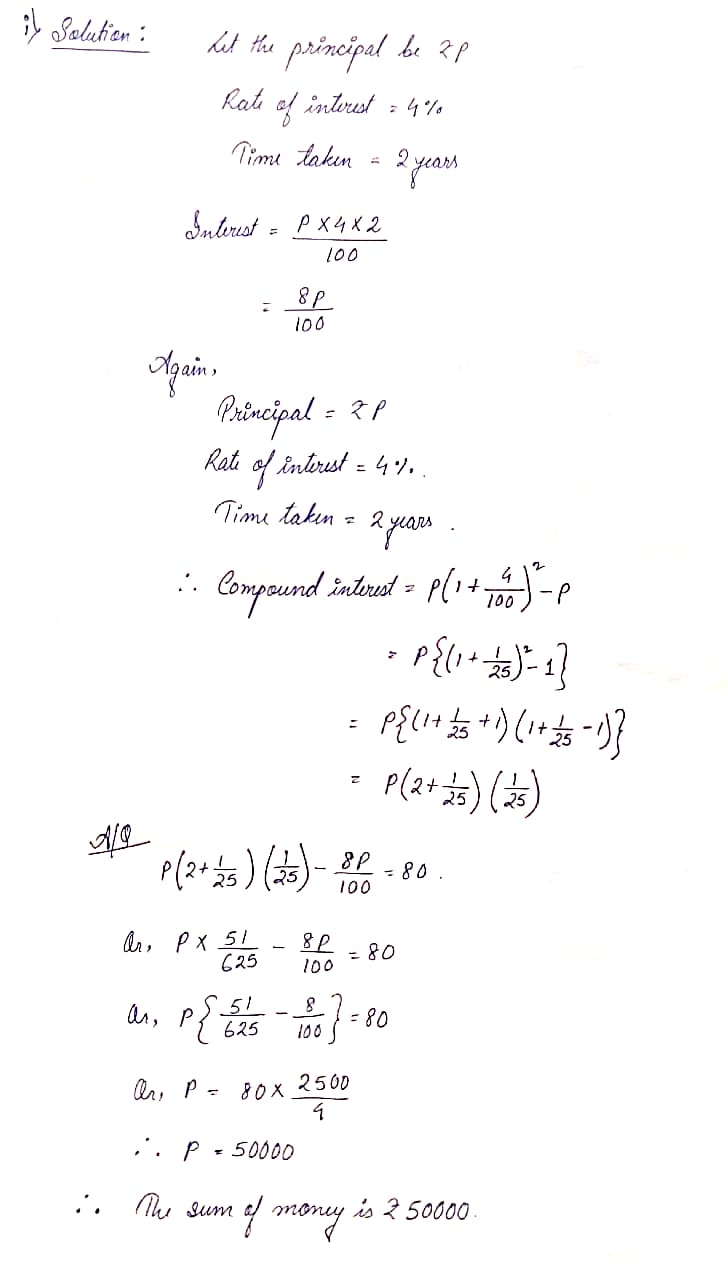
(ii) A, B, C start a business jointly investing Rs. 1,80,000 in together. A gives Rs. 20,000 more than that of B and B gives Rs 20,000 more than that of C. Distribute the profit of Rs 10, 800 among them.
Ans:


6. Solve any one:
(i) 1/(a+b+x)=1/a+1/b+1/x [x ≠ 0, (a+b)]
Ans:
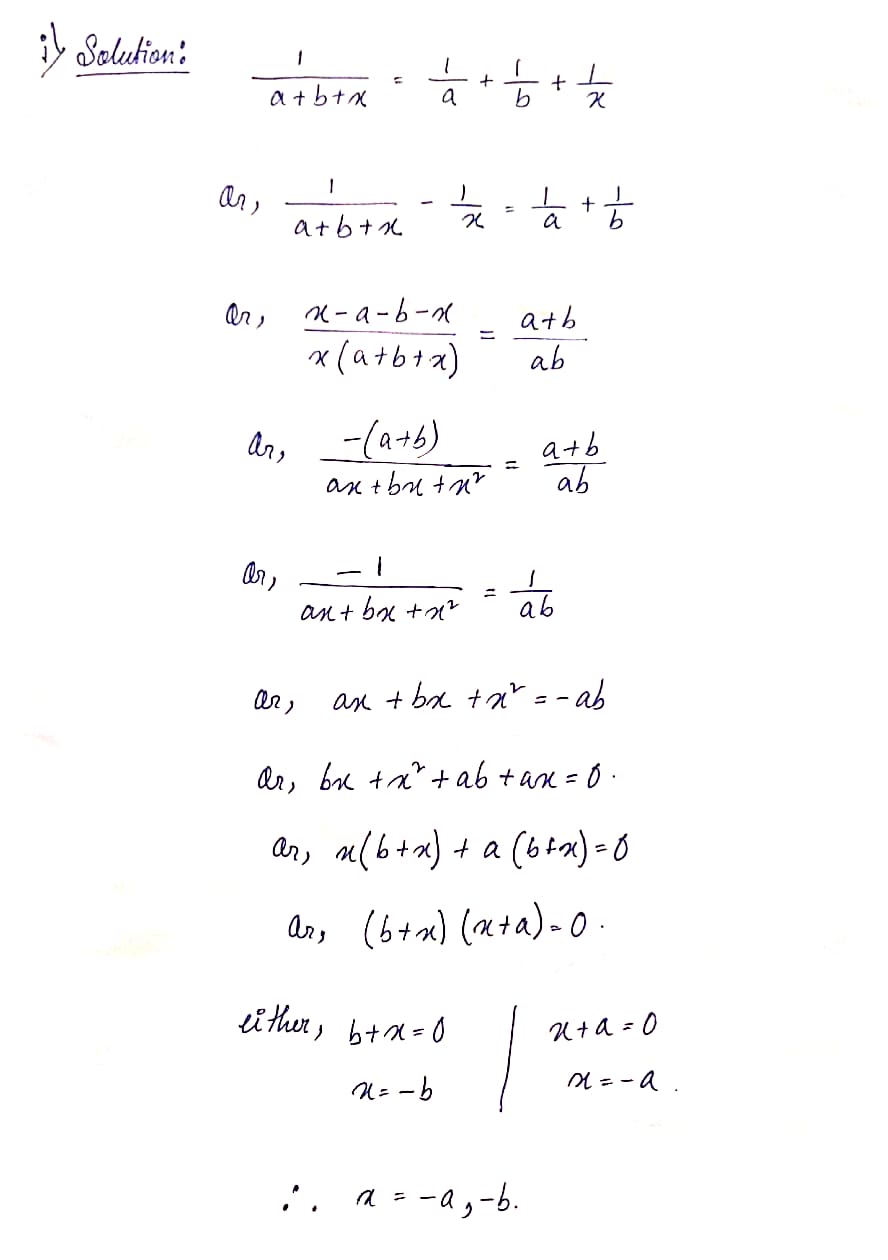
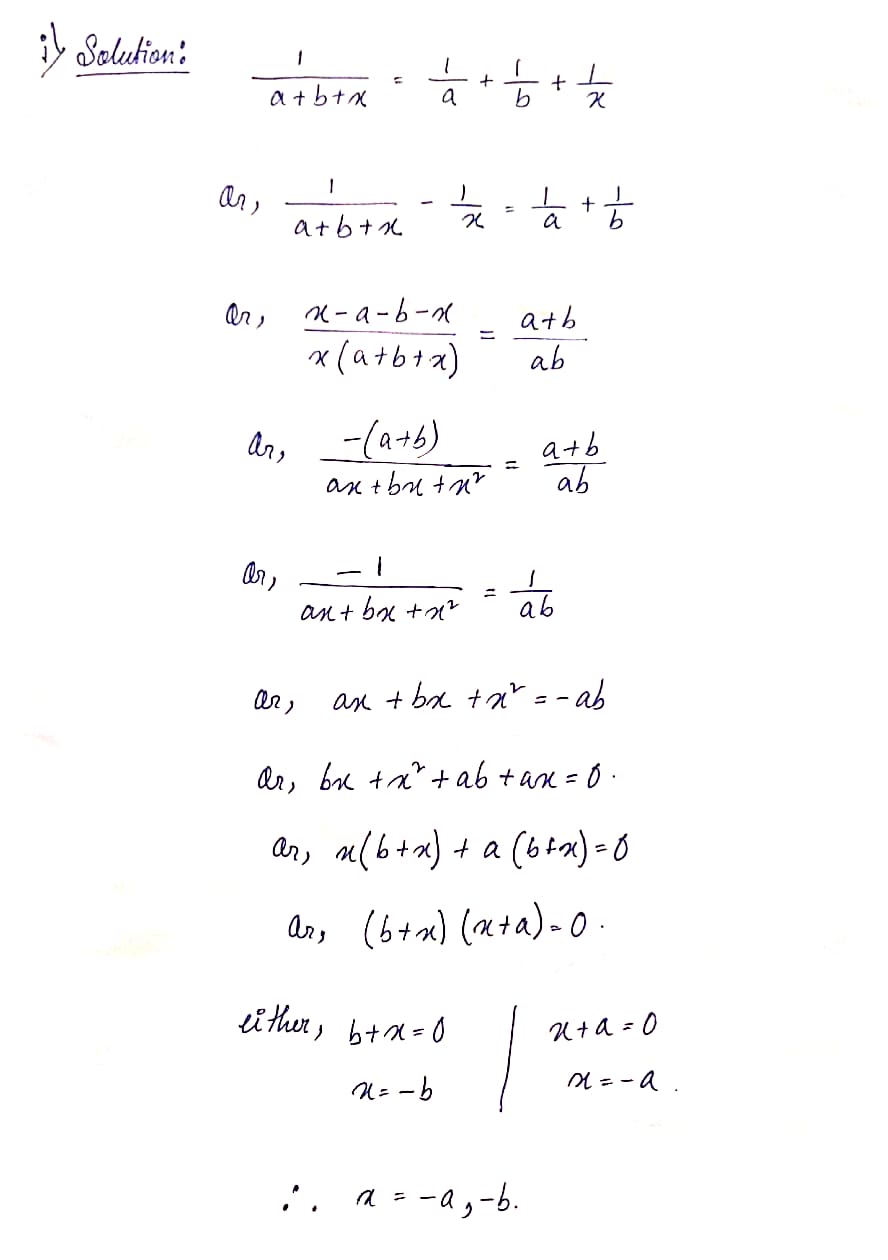
(ii) If 5 times of a positive whole number is less by 3 than twice of its square, then find the number?
Ans:


7. Answer any one:
(i) Simplify: 1/(√2+√3)-(√3+1)/(2+√3)+(√2+1)/(3+2√2)
Ans:


(ii) The total expenses of a hostel are partly constant and partly vary directly as the number of boarders. When the number of boarders are 120 and 100 the total expenses are Rs. 2,000 and Rs. 1,700 respectively. What will be the number of boarders when the total expenses is Rs.1,880?
Ans:
8. Answer any one question:
(i) If a/(b+c)=b/(c+a)=c/(a+b) then prove that each ratio is equal 1/2 or -1.
Ans:
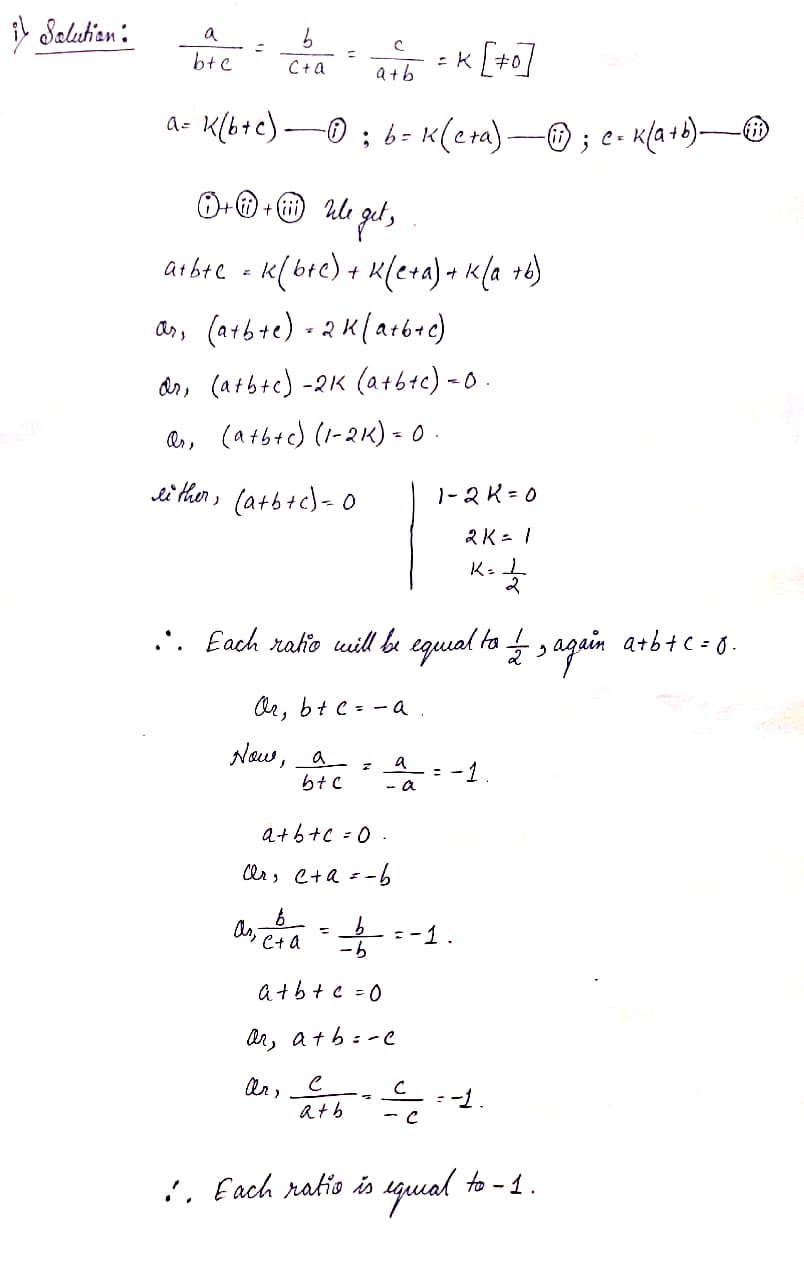
(ii) If (b+c-a)x=(c+a-b)y=(a+b-c)z=2 then show that (1/x+1/y)(1/y+1/z)(1/z+1/x)=abc
Ans:
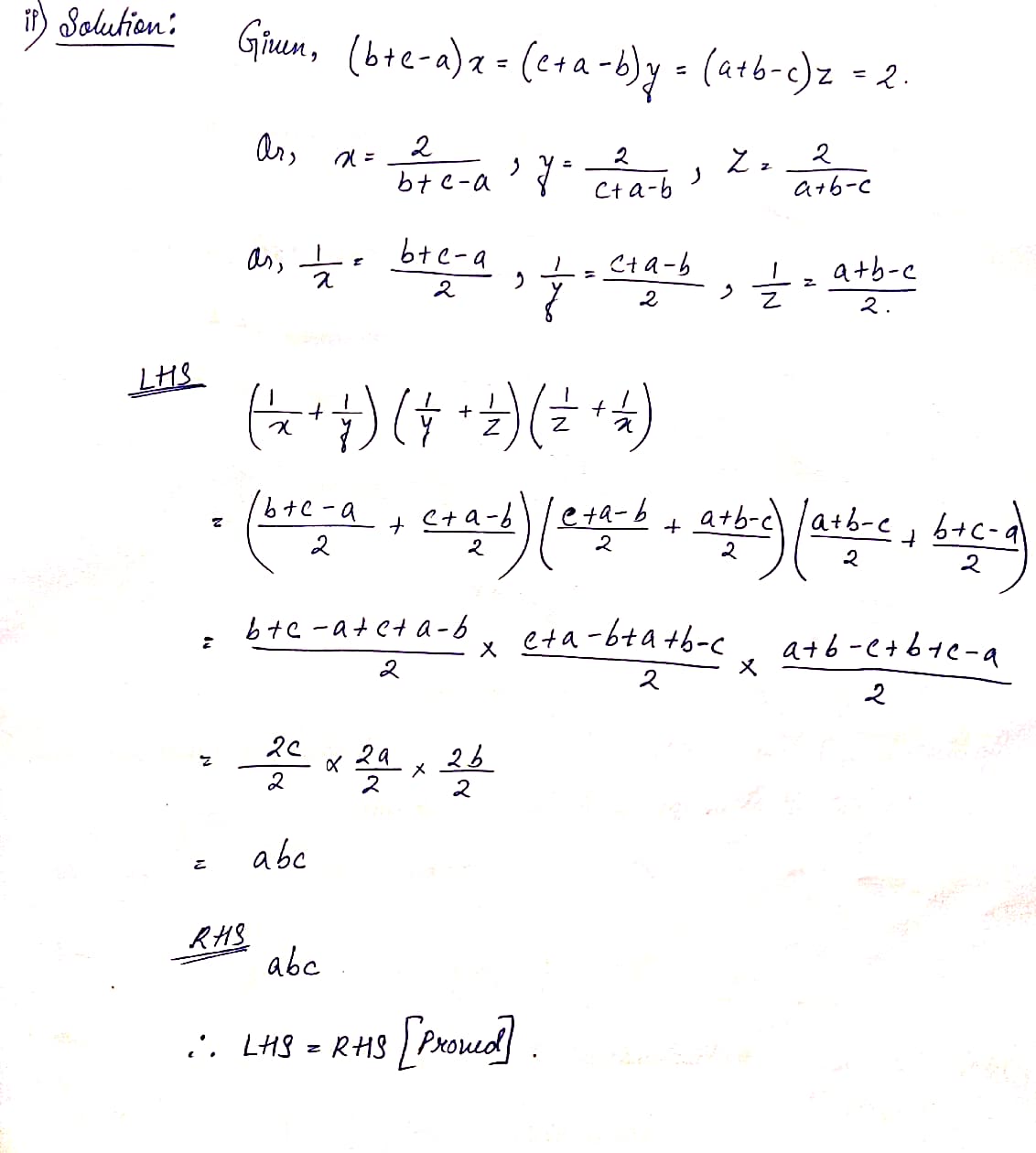
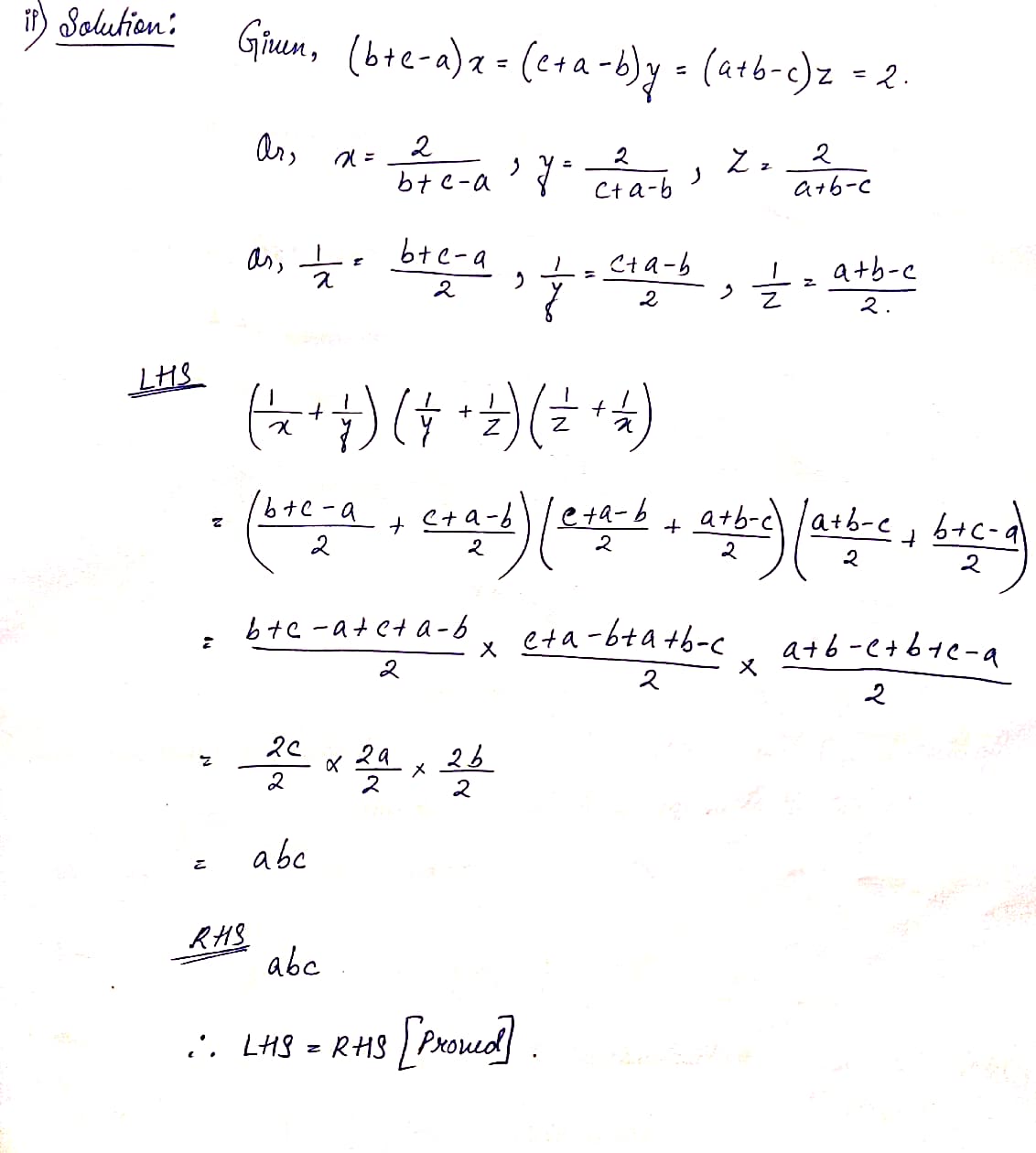
9. Answer any one question:
(i) If in a triangle, the area of the square drawn on one side is equal to the sum of the areas of squares drawn on other two sides, then prove that the angle opposite to the first side will be a right angle.
Ans:
(ii) If two tangents are drawn to a circle from a point outside it, then the line segments joining the point of contacts and the exterior point are equal.
Ans:
10. Answer any one question:
(i) Prove that the quadrilateral formed by the internal bisectors of the four angles of a quadrilateral is cyclic.
Ans:
(ii) O is the circumcentre of ∠ ABC and OD ⊥ BC; prove that ∠BOD=∠BAC.
Ans:
11. Answer any one question:
(i) Draw an equilateral triangle of side 6 cm and draw the incircle of the triangle, (only traces of construction are required.)
Ans:
(ii) Construct a rectangle with sides 8 cm and 6 cm and construct a square equal in area to that of the rectangle, (only traces of construction are required.)
Ans:
12. Answer any two questions:
(i) If the measures of three angles of a quadrilateral are π/3 ,5π/6 and 90°; then determine the fourth angle in sexagesimal and circular measure.
Ans:


(ii) If sinθ/x=cosθ/y then prove that sinθ-cosθ=(x-y)/√(x²+y²)
Ans:
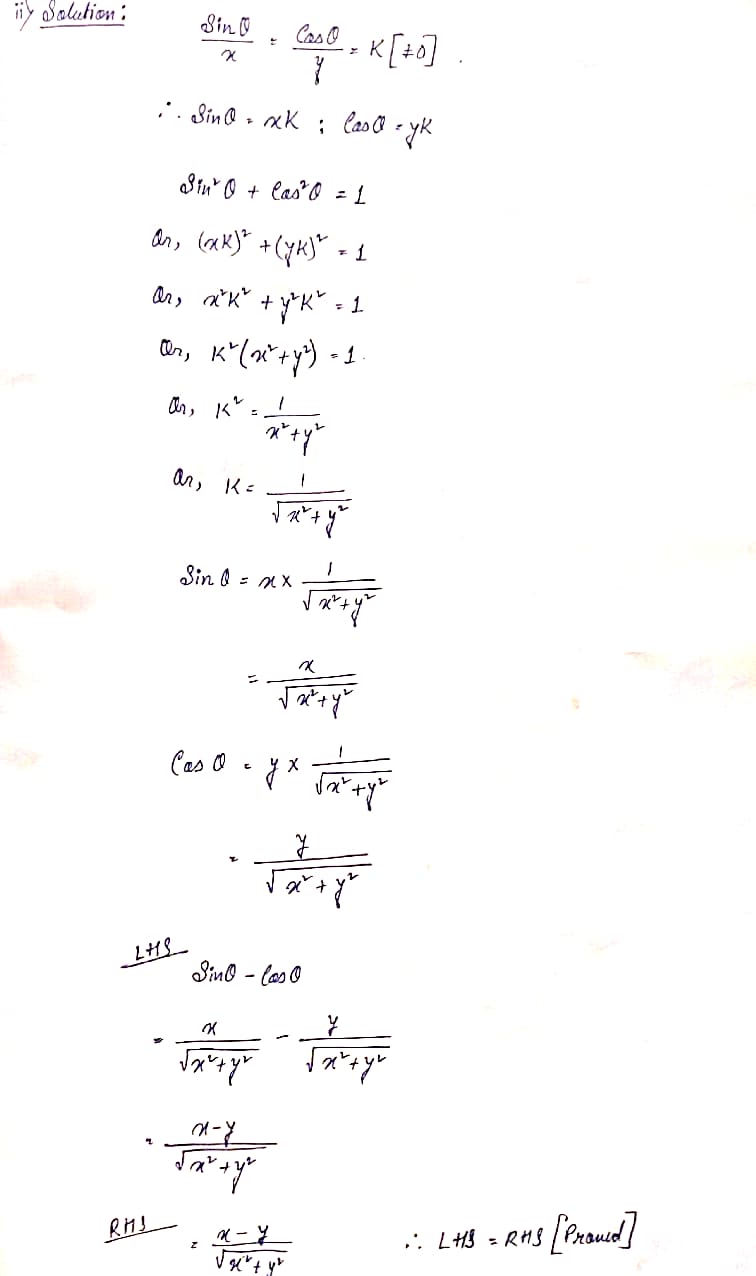
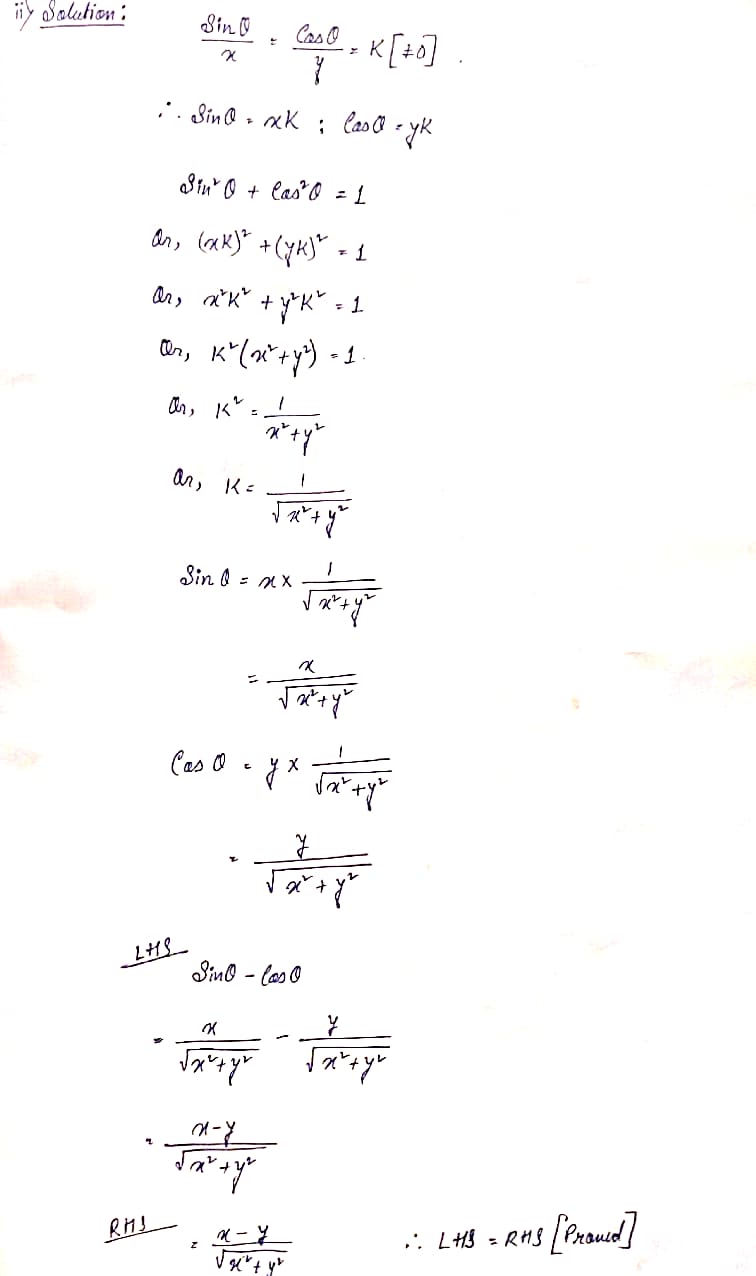
(iii) If tan 90 ° = a/b , then prove that (sec² 81°)/(1+cot² 81°)=b²/a²
Ans:
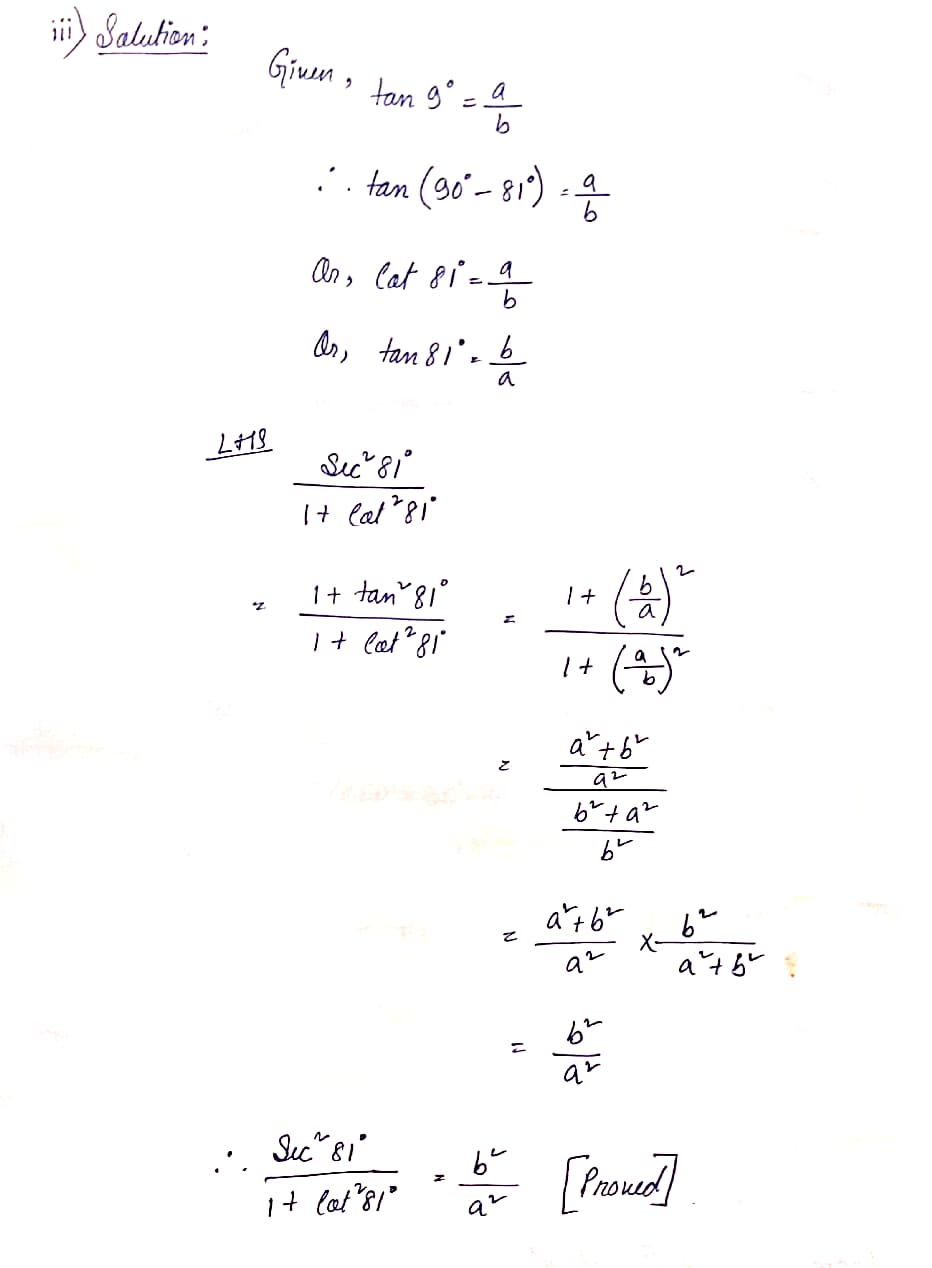
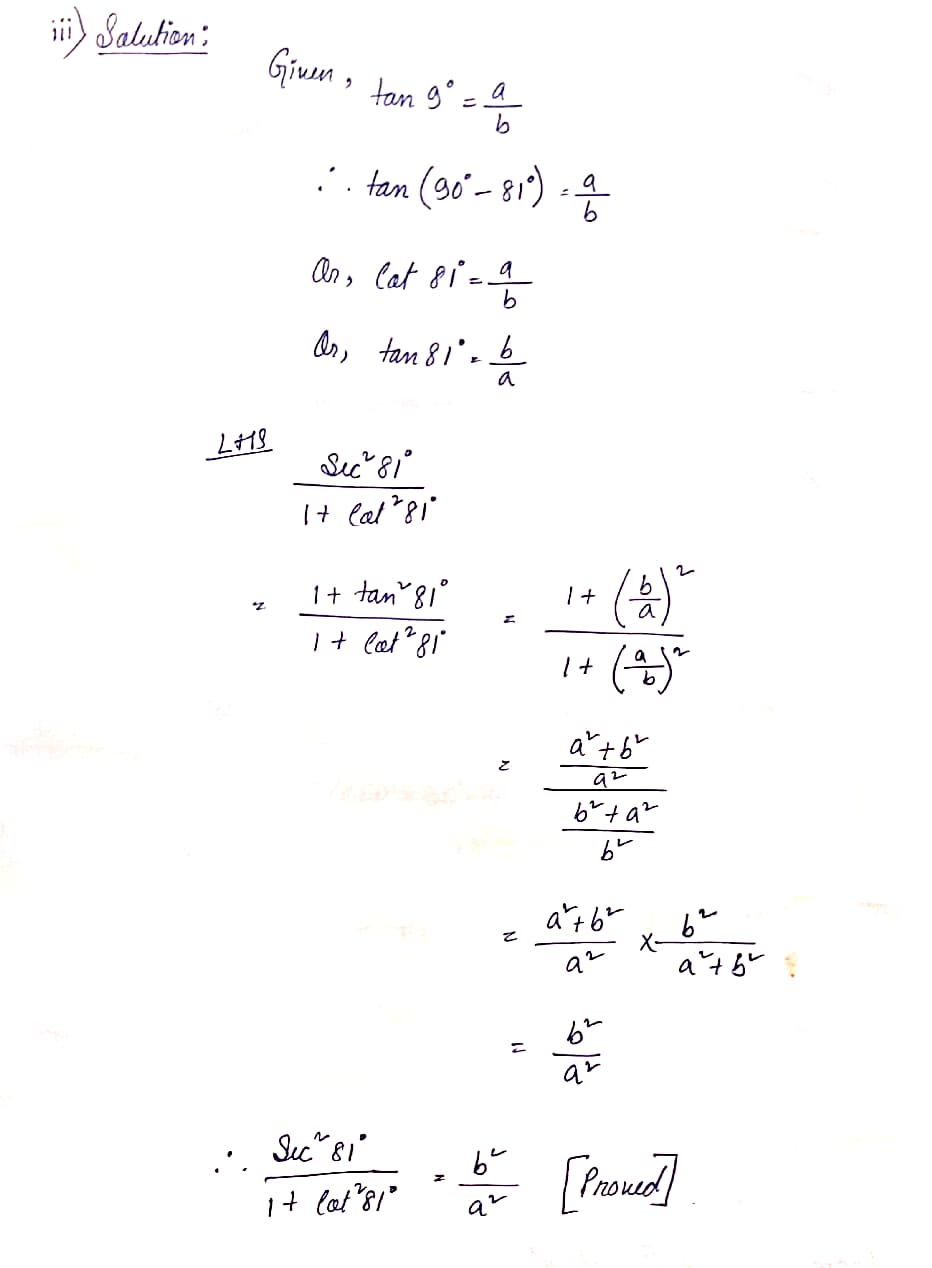
13. Answer any one question:
(i) The distance between two pillars is 150m. Height of one is thrice the other. From the midpoint of the line segment joining the foot of the pillars, the angle of elevation of the top of the pillars are complementary to each other. Find the height of the shorter pillar.
Ans:
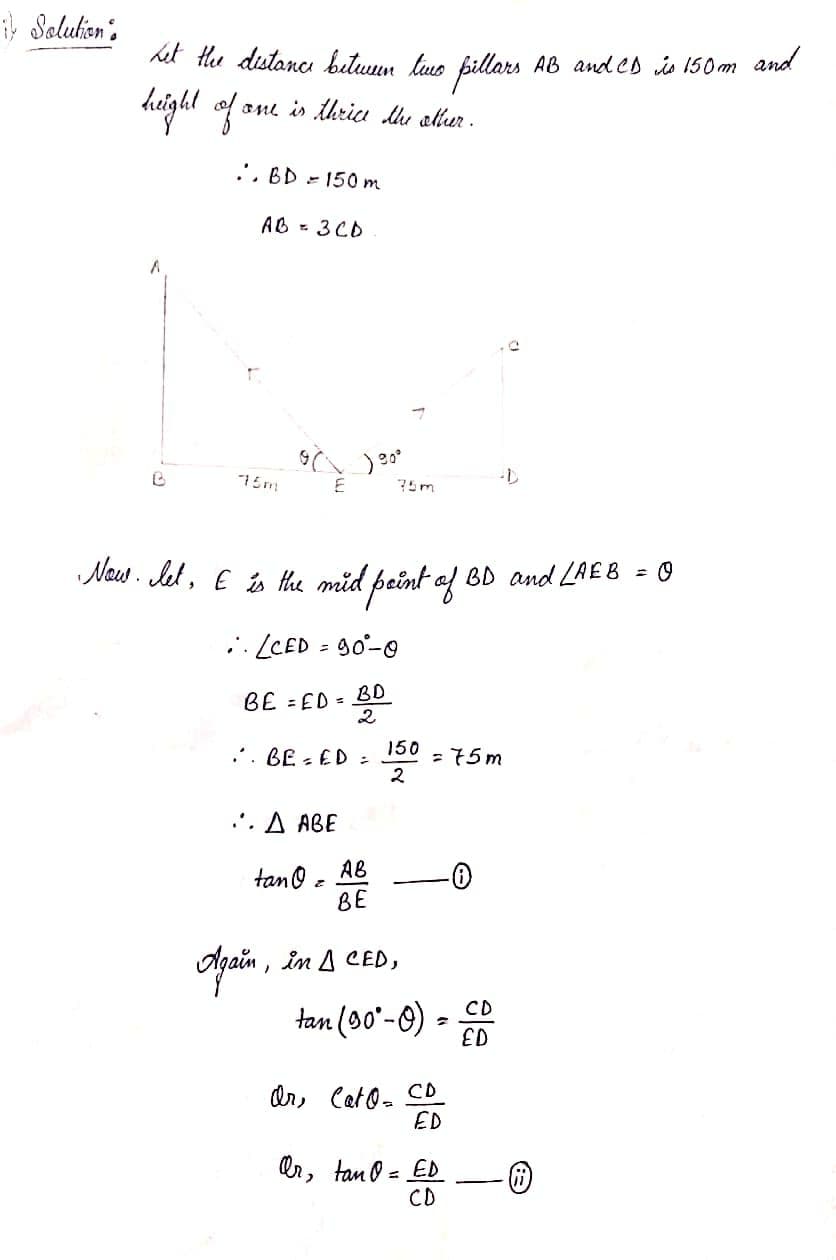
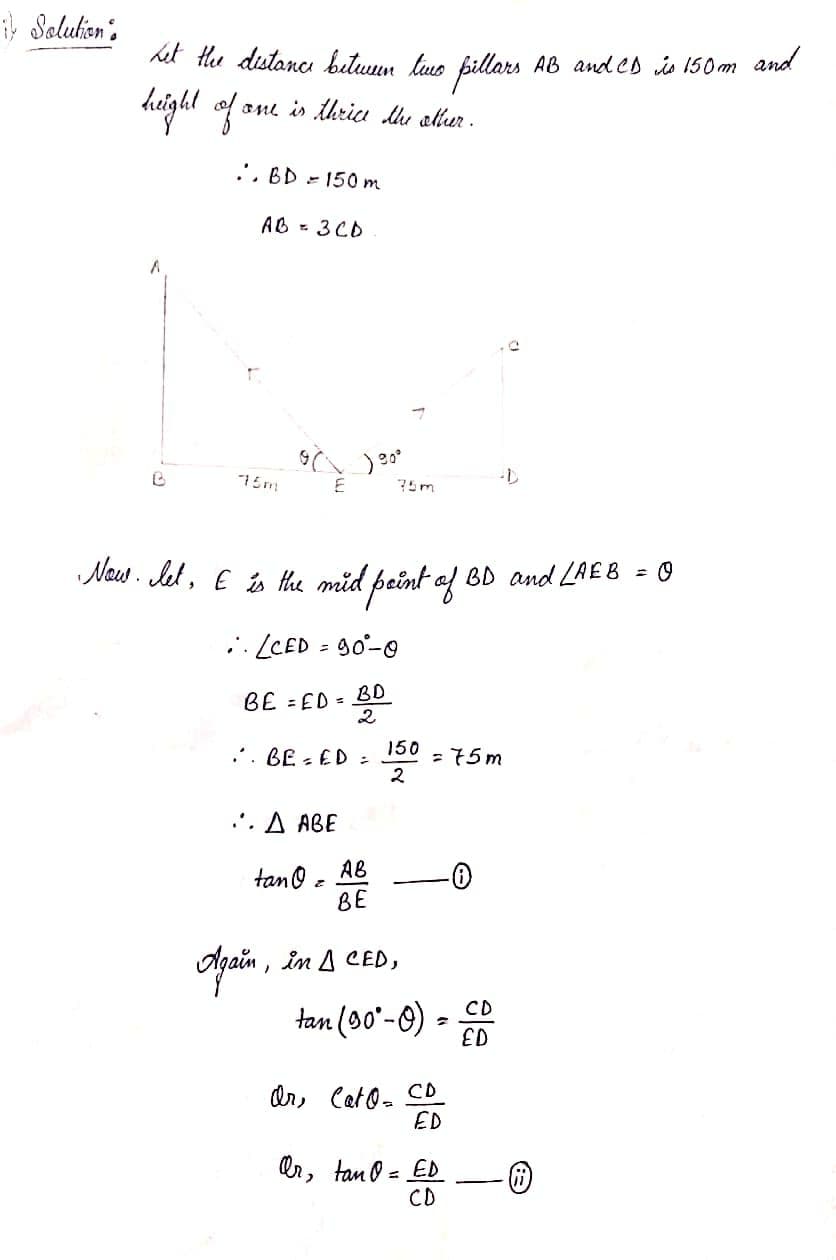


(ii) If the angle of depression from a lighthouse of two ships situated in the same line with the lighthouse are 60° and 30° and if the nearer ship, is 150 m away from the lighthouse, then find the distance of the other ship from the lighthouse.
Ans:
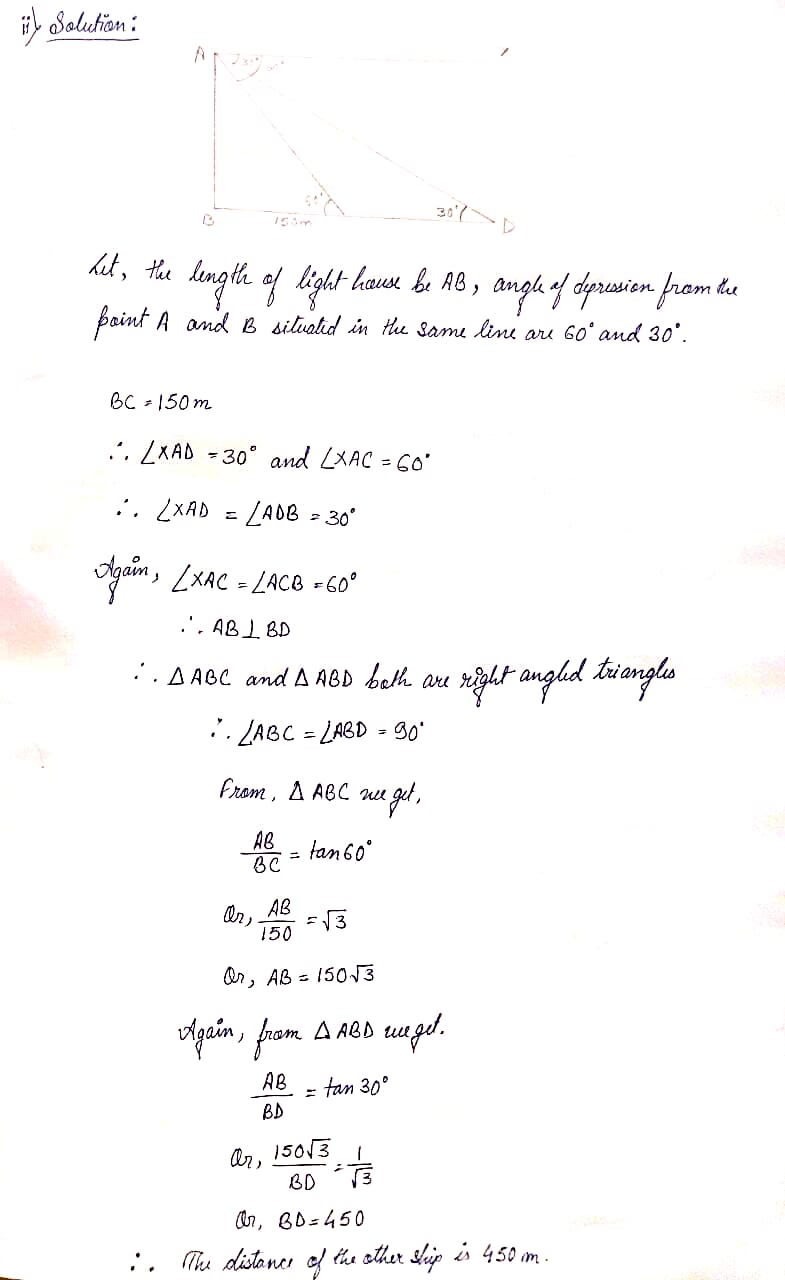
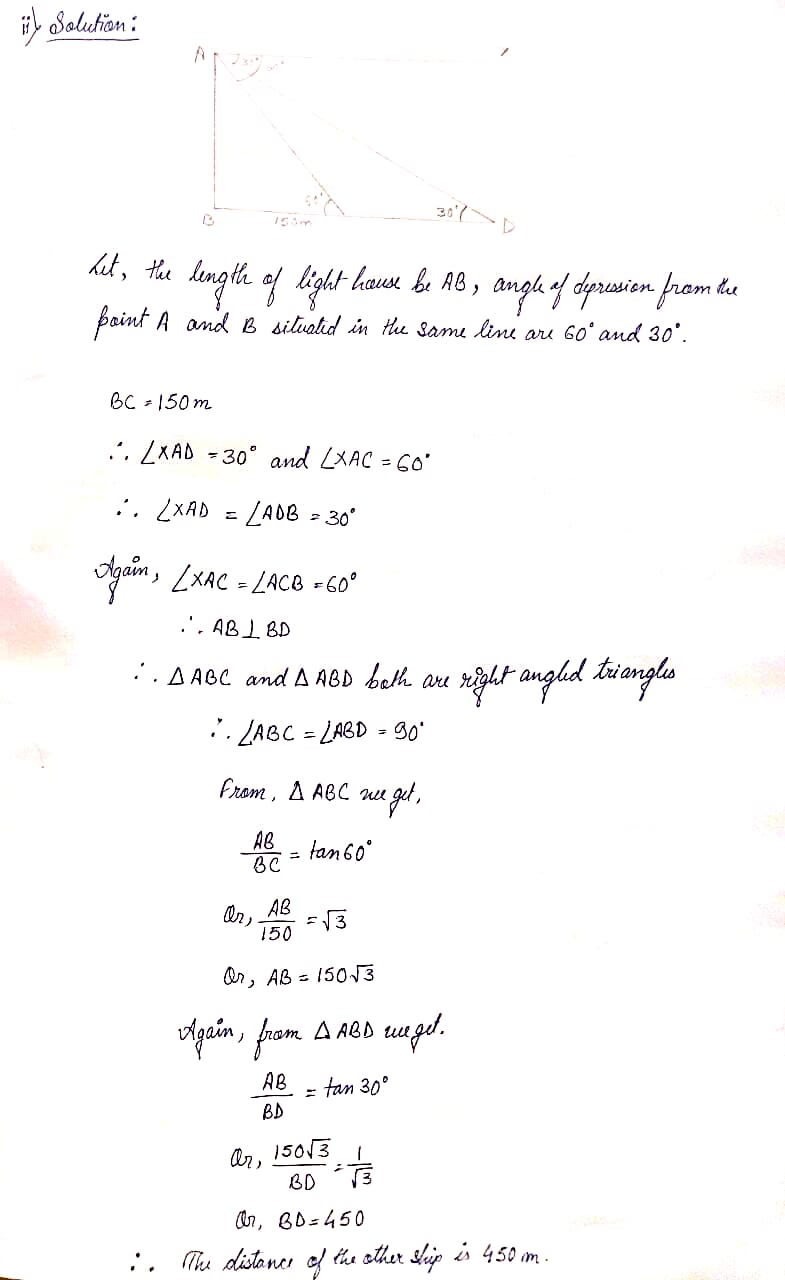
14. Answer any two questions:
(i) Determine the volume of a solid right circular cone which can be made from a solid wooden cube of 4.2 dcm edge length by wasting minimum quantity of wood.
Ans:


(ii) A hemispherical bowl with radius of 9 cm is completely filled with water. How many cylindrical bottles of diameter 3 cm and height 4cm can be filled, up with the water in the bowl.
Ans:


(iii) Area of the base of a closed cylindrical water tank is 616 sq, meter and height is 21 meters. Find the total surface area of the tank.
Ans:


15. Answer any two questions:
(i) If the median of the following data is 32, fund the values of x and y when the sum of the frequencies is 100.




(ii) Find the mode from the following distribution table:


(iii) By preparing a cumulative frequency (greater than type) table from the following data, draw a ogive in a graph paper.



